Rozdział 2 Podstawy R

Praca w środowisku R możliwa jest w dwóch podstawowych trybach: skryptowym (wsadowym) oraz interaktywnym. Tryb interaktywny jest mniej skomplikowany i od niego rozpoczniemy naszą naukę. Praca w tym trybie polega na wprowadzaniu komend do konsoli (interpretera języka programowania), który znajduje się domyślnie po lewej stronie okna programu RStudio.

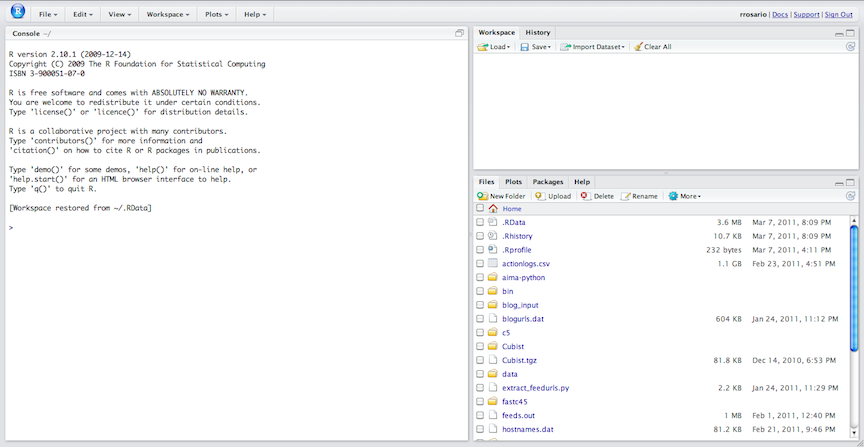
Ekran początkowy programu RStudio

Ekran początkowy programu RStudio

2.1 Terminal R

W konsoli R możemy wpisywać komendy, a po naciśnięciu klawisza Enter komendy te są przez komputer interpretowane. Jeśli polecenie jest poprawne komputer obliczy jego rezultat. Alternatywnie informacja zwrotna o napotkanym błędzie wyświetlana jest jako error lub w formie ostrzeżenia (ang. warning)). Spróbujmy wykorzystać R jako kalkulator i przetestujmy zachowanie terminala.

5+3
## [1] 8

Brak informacji o błędzie oznacza poprawne wykonanie działania. Obok wyniku w nawiasie kwadratowym komputer zwrócił liczbę porządkową pierwszej wartości w danym wierszu.

5+2,5
## Error: <text>:1:4: unexpected ','
## 1: 5+2,
##        ^

Komunikat błędu wskazuje miejsce jego wystąpienia. W tym przypadku jest to przecinek, który nie pasuje do składni interpretowanego polecenia, ponieważ separatorem miejsc dziesiętnych w R jest kropka a nie przecinek.

Jeśli chcemy szybko poprawić ten błąd możemy użyć kursorów (strzałek) na klawiaturze góra-dół do przeglądania ostatnio wprowadzonych poleceń i kursorami lewo-prawo przenieść się do miejsca wymagającego poprawy.

Zwróć uwagę, że jeśli komenda jest (przynajmniej częściowo) poprawna, ale nie zostanie zakończona w danej linii, wówczas po naciśnięciu Entera zamiast tzw. znaku zachęty ">" zostanie zwrócony znak "+".

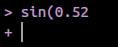
Przykład niepoprawnie zakończonej komendy (brak znaku ) ), i pojawienie się znaku + w nowej linii konsoli oznaczający możliwość dokończenia wpisywanej komendy

Przykład niepoprawnie zakończonej komendy (brak znaku “)” ), i pojawienie się znaku “+” w nowej linii konsoli oznaczający możliwość dokończenia wpisywanej komendy

W takiej sytuacji możliwe są 2 rozwiązania - dokończenie wpisywania poprzedniej komendy, lub naciśnięcie klawisza Esc w celu przerwania bieżącego procesu. Klawisz Esc (lub ikonkę symbolizującą znak STOP) można nacisnąć zawsze w celu przerwania aktualnie aktywnego procesu.

Zadanie:

Sprawdź powyższe działania terminala testując polecenie: 6+ (Enter), w kolejnej linii wprowadź dowolną liczbę i ponownie naciśnij Enter. Za drugim razem wpisz 6+ (Enter), ale tym razem przerwij działanie stosując Esc.

 

 

2.2 Arytmetyka

Wykonaj poniższe zadania sprawdzające działanie R jako kalkulatora:

  1. Oblicz wyrażenie 2+3*5
  2. Stosując nawiasy, które pozwalają na zmianę domyślnej kolejności wykonywania działań zmodyfikuj powyższe działanie w taki sposób, aby najpierw była wykonywane sumowanie, a dopiero potem mnożenie (tj., końcowy wynik powinien dać 25)
  3. Pomnóż liczby 3 i 5
  4. Podziel dowolne 2 liczby
  5. Sprawdź działanie operatorów %% oraz %/% na dowolnych dwóch liczbach całkowitych. Do czego one służą?
  6. Sprawdź działanie operatora ^

Jeśli chcesz obliczyć wynik funkcji wykładniczej (exp), sinusa (sin), cosinusa (cos), pierwiastka kwadratowego (sqrt), logarytmu dziesiętnego (log), wartości bezwzględnej (abs), wartości maksymalnej (max), minimalnej (min), średniej (mean), odchylenia standardowego (sd), itp., musisz zastosować składnię funkcyjną, o której powiemy nieco później. W najprostszej postaci należy wprowadzić nazwę funkcji i w nawiasie podać argument dla funkcji, czyli w tym przypadku liczbę.

UWAGA! Wielkość znaków w R MA ZNACZENIE! (czyli LOG to dla komputera coś innego niż log).

W RStudio bardzo przydatny jest klawisz tabulatora, który pozwala na uzupełnienie nazwy funkcji lub obiektu po naciśnięciu klawisza TAB. W ten sposób np. po wpisaniu liter sq i naciśnięciu TAB pojawi się intuicyjne okno z podpowiedzią.

  1. Na podstawie powyższych informacji oblicz:
  • Pierwiastek z 9
  • Cosinus liczby pi, gdzie pi jest stałą wbudowaną w R (wystarczy wpisać pi zamiast 3.141593)
  1. W jednej linii kodu podnieś liczbę 9 do kwadratu i oblicz pierwiastek kwadratowy (sqrt) z tej liczby. Podpowiedź: funkcje mogą być wzajemnie zagnieżdżone

Wskazówka: Przy interpretacji polecenia R pomija spacje pomiędzy poszczególnymi elementami działania. NIE JEST istotne czy twoja komenda jest zapisana jako 5+4.5 czy 5 + 4.5 (ale nie możesz wpisać spacji przy liczbach, np.: 5+4 .5 !).

2.3 Tworzenie obiektów

Dotychczas wynik naszego polecenia wyświetlał się na ekranie, ale nie mogliśmy z nim dalej nic zrobić, bo nie był zapisywany w pamięci komputera. Wpisywanie komend w terminalu i sprawdzanie ich wyniku nie jest zbyt efektywne, dlatego też większość pracy w R odbywa się na obiektach. Czym jest obiekt? W bardzo dużym skrócie to po prostu nazwa do której przypisuje się wartość. Nazwa nie może się zaczynać od liczb oraz znaków specjalnych. Najlepiej także unikać polskich znaków.

W R istnieje kilka sposobów tworzenia obiektów (zmiennych). Najczęściej stosowanym operatorem przypisania jest wyrażenie <-, które w RStudio możemy otrzymać za pomocą skrótu lewy Alt + -. Warto dobrze zapamiętać ten skrót.

Obiekt można stworzyć także za pomocą operatora =, który działa analogicznie jak <-. Ze względu na pewne uwarunkowania historyczno-techniczne bardziej rekomendowany jest zapis w postaci strzałki. Wyrażenie można przypisać także prawostronnie za pomocą operatora -> . Choć jest to poprawna forma zapisu, w praktyce jest rzadko stosowana.

Stwórzmy zatem naszą pierwszą zmienną, którą nazwiemy temperatura i przypiszmy jej wartość 279.15:

temperatura <- 279.15

Zauważ, że w prawym górnym rogu okna RStudio w zakładce Environment pojawiła nazwa zdefiniowanej zmiennej i jej wartość. W tej zakładce będą pojawiać się wszystkie nazwy stworzonych lub wczytanych obiektów.

W odróżnieniu od wcześniejszych zastosowań R jako kalkulatora nie wyświetlił nam się wynik tej operacji. To dlatego, że zapisaliśmy go w pamięci komputera. Brak informacji zwrotnej jednocześniej oznacza, że operacja przebiegła poprawnie.

Jeśli chcemy wyświetlić zawartość naszej zmiennej możemy wpisać po prostu jej nazwę lub wykorzystać funkcję print (pamiętaj o używaniu TABulatora!):

temperatura
## [1] 279.15
print(temperatura)
## [1] 279.15

Pamiętaj, że wielkość znaków w R MA ZNACZENIE, tzn. wyrażenie temperatura i Temperatura to dla komputera 2 różne obiekty!

Wyobraźmy sobie, że wartość przechowywana w obiekcie temperatura to temperatura powietrza wyrażona w Kelwinach (podstawowa jednostka układu SI). Jeśli chcemy przeliczyć Kelwiny na stopnie Celsjusza musimy zastosować poniższe równanie (2.1):

\[\begin{equation} T(^\circ C) = K-273.15 \tag{2.1} \end{equation}\]

W tym momencie można wykorzystać zawartość zmiennej temperatura aby podstawić ją do równania i zapisać wynik działania do obiektu, który nazwiemy tc (temperatura w Celsjuszach):

tc <- temperatura-273.15

Zadanie:

  1. Stosując poniższy wzór na przeliczenie temperatury ze stopni Celsjusza na temperaturę w Fahrenheitach utwórz obiekt tf. Wartość temperatury przelicz ze zmiennej tc
\[\begin{equation} T(^\circ F) = T(^\circ C) * 1.8 + 32 \tag{2.2} \end{equation}\]

  1. Na nowym obiekcie tf sprawdź działania funkcji matematycznych floor, ceiling oraz round.

  2. Sprawdź co stanie się po wywołaniu komendy ?round oraz ??"ceiling" ?

 

 

2.4 Generowanie ciągów liczbowych

Praca na obiektach przechowujących jedną wartość nie daje zbyt wielkich korzyści. Obiekty R mogą przechowywać znacznie więcej wartości i aby się o tym przekonać poznamy 3 podstawowe schematy generowania ciągów liczbowych:

  1. Za pomocą : możemy stworzyć ciąg liczb z interwałem co 1. W zależności od tego jakie wartości podstawimy z prawej i lewej strony dwukropka będzie to ciąg rosnący lub malejący:
150:180
##  [1] 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166
## [18] 167 168 169 170 171 172 173 174 175 176 177 178 179 180
5:-20
##  [1]   5   4   3   2   1   0  -1  -2  -3  -4  -5  -6  -7  -8  -9 -10 -11
## [18] -12 -13 -14 -15 -16 -17 -18 -19 -20
11.375:34
##  [1] 11.375 12.375 13.375 14.375 15.375 16.375 17.375 18.375 19.375 20.375
## [11] 21.375 22.375 23.375 24.375 25.375 26.375 27.375 28.375 29.375 30.375
## [21] 31.375 32.375 33.375
  1. Podobnie do powyższego schematu działa funkcja seq. Szczegóły jej działania można znaleźć po wywołaniu komendy ?seq (dostęp do systemu pomocy). Zgodnie z uzyskanymi informacjami z systemu pomocy - jeśli chcemy wygenerować ciąg liczb od 0 do 20 co 1 komenda będzie wyglądała następująco
seq(from=0, to=20, by=1)
##  [1]  0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

Jeśli nie wiemy jaki powinien być interwał pomiędzy liczbami, ale znamy długość generowanego ciągu opcję by możemy zastąpić opcją length.out. Jeśli chcemy wygenerować 35 liczb w równych odległościach od 0 do 20, wówczas możemy zastosować poniższy kod:

seq(from=0, to=20, length.out =35)
##  [1]  0.0000000  0.5882353  1.1764706  1.7647059  2.3529412  2.9411765
##  [7]  3.5294118  4.1176471  4.7058824  5.2941176  5.8823529  6.4705882
## [13]  7.0588235  7.6470588  8.2352941  8.8235294  9.4117647 10.0000000
## [19] 10.5882353 11.1764706 11.7647059 12.3529412 12.9411765 13.5294118
## [25] 14.1176471 14.7058824 15.2941176 15.8823529 16.4705882 17.0588235
## [31] 17.6470588 18.2352941 18.8235294 19.4117647 20.0000000
  1. Losowe ciągi liczbowe można także wygenerować za pomocą funkcji z wybranych rozkładów statystycznych. Jednym z najbardziej przydatnych jest rozkład jednostajny ciągły, który w R jest wbudowany do funkcji runif lub rozkład normalny (rnorm). Przykładowo, jeśli chcemy wygenerować 5 losowych liczb w przedziale od 1 do 10, wówczas kod wygląda następująco:
runif(5, min=1, max=10)
## [1] 3.617465 5.332572 2.846467 6.772858 3.261791

Zadanie:

  1. W arkuszach kalkulacyjnych można wygenerować narastający ciąg liczbowy chwytając za róg komórki z wartością i przesuwając ją w dół. Gdybyś chciał wygenerować liczby od 1 do samego dołu arkusza kalkulacyjnego zajęło by to prawdopodobnie dużo czasu. Stwórz analogiczny schemat postępowania w R aby wygenerować ciąg liczb od 1 do 1048576 i zapisz ten wynik do obiektu a. Które z rozwiązań jest szybsze?

  2. Dla chętnych: Sprawdź ile danych w ciągu narastającym od 1 możesz wygenerować i zapisać do obiektu a zanim braknie komputerowi pamięci? Do testów wykorzystaj wielokrotność potęgi 2 (np. 2^20, 2^35). Ile było by potrzebnych arkuszy kalkulacyjnych do przechowania takiej liczby danych gdyby każda liczba była zapisana w nowym rzędzie?

  3. Stworzony obiekt niemal w całości wypełnia dostępną pamięć RAM naszego komputera. Usuń stworzony obiekt za pomocą funkcji rm(a)

  4. Korzystając ze wzoru przeliczającego temperaturę ze stopni Celsjusza na stopnie Fahrenheita (2.2) wygeneruj wartości temperatury w stopniach Celsjusza od -10 do +30 i oblicz ich wartości w stopniach Fahrenheita

  5. Wygeneruj losowo 50 liczb o wartościach od 0 do 1 z rozkładu jednostajnego i oblicz wartość średnią. Funkcja do obliczania średniej arytmetycznej nazywa się mean.

 

 

2.5 Łączenie obiektów

Tworzenie obiektów jest możliwe także za pomocą operatora c(), który w R pozwala na sklejanie dwóch lub więcej wyrażeń (np. liczbowych) w jedno. Fachowo taka operacja złączająca nazywa się konkatenacją.

Funkcja c() jest bardzo prosta w swoim działaniu i wymaga podania kolejnych złączanych obiektów rozdzielonych przecinkami. Najlepiej zaznajomić się z konkatenacją na przykładach:

  1. Utwórz obiekt a, który będzie przechowywał wartości liczbowe 1,2,3,5
a <- c(1,2,3,5)
  1. Utwórz obiekt b, który będzie zawierać wartości od 0 do 10 co 1 oraz od 10 do 1 co 1. Wykorzystaj do tego celu operator :
b <- c(0:10,10:1)
  1. Złącz obiekty a i b, na końcu dołącz obiekt b powiększony o 20
c(a, b, b+20)
##  [1]  1  2  3  5  0  1  2  3  4  5  6  7  8  9 10 10  9  8  7  6  5  4  3
## [24]  2  1 20 21 22 23 24 25 26 27 28 29 30 30 29 28 27 26 25 24 23 22 21
  1. Oblicz odchylenie standardowe (z ang. standard deviation) liczb 0,5,-2,4
sd(c(0,5,-2,4))
## [1] 3.304038

Zwróć uwagę, że aby wykonać prawidłowo operację na obiekcie zawierającym więcej niż 1 element konieczna jest jego wcześniejsza konkatenacja (jak w powyższym przykładzie).

Zadania sprawdzające