Rozdział 3 Podstawy R - część 2

3.1 R skrypt

Na poprzednich zajęciach praca z R opierała się na wprowadzaniu komend do terminala, gdzie były one natychmiast przetwarzane przez komputer. W praktyce rzadko się zdarza, że cały proces przetwarzania danych czy tworzenia własnego algorytmu można sprowadzić do kilku- kilkunastu linii kodu. Dlatego też ciąg wydawanych poleceń zapisywany jest najczęściej jako plik skryptowy R, który pozwala na:

  • łatwiejsze uporządkowanie kolejnych poleceń w logiczny ciąg przetwarzania danych
  • w razie znalezienia błędu - łatwiej jest poprawić taki kod widząc cały schemat postępowania od początku do końca
  • każdą linię kodu możemy automatycznie uruchomić i sprawdzić jaki daje wynik.

Utworzenie nowego pliku skryptowego w programie RStudio możliwe jest za pomocą:

  • wybrania z górnego menu opcji File, następnie opcji New File oraz R Script (jak pokazano w przykładzie)
  • poprzez skrót klawiszowy ctrl+shift+n
  • wybierając ikonę białej kartki z zielonym kółkiem i znakiem plusa. Ikona znajduje się skrajnie z lewej w pierwszym rzędzie ikon. Po wysunięciu szeregu opcji należy wybrać pierwszą z nich, tj. R Script.
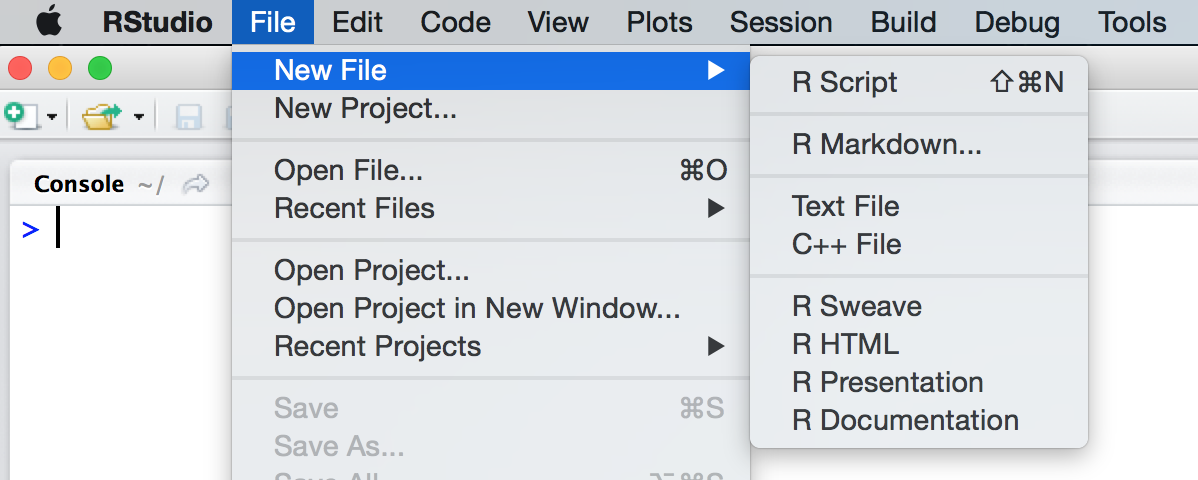
Tworzenie nowego skryptu R w interfejsie programu RStudio

Tworzenie nowego skryptu R w interfejsie programu RStudio

Lewe okno programu RStudio powinno podzielić się na 2 mniejsze, z dotychczasowym terminalem na dole i nowym oknem do wpisywania skryptu u góry.

Plik skryptowy R jest zwykłym plikiem tekstowym z rozszerzeniem .r lub .R. Określenie “zwykły plik tekstowy” oznacza, że zawiera on tylko te informacje, które są widoczne na ekranie. To trochę tak, jakby wszystkie nasze dotychczasowe komendy wpisywane w terminalu zapisać w “notatniku”, a następnie wklejać je w zależności od potrzeb do terminala.

Jak działa skrypt R?

Aby “przenieść” daną linię kodu z okna skryptowego do terminala i ją wykonać należy posłużyć się skrótem ctrl+enter. Wówczas aktywna linia kodu zostanie przeniesiona do terminala i wykonana.

Jeśli chcemy jednorazowo uruchomić więcej niż 1 linię kodu (np. jedno polecenie rozpisaliśmy w kilku liniach) możemy zaznaczyć je myszką (lub za pomocą strzałek i shift), a następnie wykonać ten blok kodu stosując skrót ctrl+enter. Częste stosowanie tego skrótu sprawi, że część osób nazwie te zajęcia “ctrl+enter” ;)

Docelowo będziemy dążyć do postaci, w której cały stworzony skrypt stanowi spójną całość i może być uruchomiony linia po linii od początku do końca. Zamiast wielokrotnego wciskania ctrl+enter linia po linii (lub zaznaczenia całego kodu i naciśnięcia ctrl+enter) można ten sam efekt uzyskać za pomocą ikony Source znajdującej się w prawym górnym rogu okna skryptowego (skrót: ctrl+shift+s). Jest to równoznaczne z użyciem funkcji source(nazwa_naszego_pliku_skryptowego.R).

3.2 Praca ze skryptem

Praca ze skryptami wymaga wyrobienia pewnych nawyków, które pozwolą na bardziej efektywne tworzenie kodu i przetwarzanie danych.

3.2.1 Komentarze

Komentarz to fragment kodu znajdujący się bezpośrednio po znaku #, który nie jest interpretowany przez komputer podczas wykonywania danego polecenia. W środowisku RStudio najczęściej po znaku komentarza zmienia się kolor składni dający do zrozumienia użytkownikowi, że dalszy fragment kodu to właśnie komentarzem:

length(-5:5) # funkcja "length" zwraca liczbę elementów / tu: długość ciągu liczbowego
## [1] 11

Dobrym zwyczajem, zwłaszcza na początku nauki programowania i/lub przetwarzania danych jest tworzenie możliwie obszernych i precyzyjnych komentarzy ułatwiających zrozumienie naszego działania lub poszczególnych bloków kodu.

Jedna ze szkół programowania zakłada, że “z komentarzy powinno się móc wywnioskować wszystko co program robi, bez oglądania reszty źródeł” (Dewhurst and Stark 1995). Stosowanie tej zasady pozwoli na dużą oszczędność czasu, zwłaszcza jeśli nasz skrypt:

  • jest używany do nauki programowania/przetwarzania danych,
  • jest stosunkowo skomplikowany,
  • zawiera wiele nowych elementów,
  • jest otwierany stosunkowo rzadko,
  • ma być docelowo używany także przez inne osoby.

Komentarze warto stosować także w odniesieniu do pewnych fragmentów testowanego kodu, które chcemy chwilowo wyłączyć, ale nie chcemy się ich na stałe pozbywać. Twórcy RStudio pomyśleli o takim zastosowaniu dając użytkownikom skrót ctrl+shift+c, który w zaznaczonym fragmencie kodu na początku każdej linii tworzy znak komentarza. W celu przetestowania tego rozwiązania stwórz poniższy fragment kodu nawiązujący do przeliczeń temperatury powietrza z stopni Celsjusza na stopnie Fahrenheita:

tc <- -20 # wartosc temperatury w *C 
tf <- tc*1.8+32 # przeliczamy na stopnie F
print(tf) # wyświetlamy zawartość zmiennej tf

tc <- -10:10 # za drugim razem chcemy przetestowac zakres wartosci temperatury w *C od -10 do +10
tf <- tc*1.8+32 # znowu przeliczamy na stopnie F
print(tf) # wyświetlamy zawartość zmiennej tf

A następnie zaznacz ostatnie 3 linie kodu i zakomentuj skrótem ctrl+shift+c. Uruchom cały kod (łącznie z zakomentowanymi liniami) i dla pewności sprawdź wartości przechowywane w zmiennych.

3.3 Wektory i podstawowe operacje na wektorach

Podstawowym typem obiektu w R są wektory. Znasz je już z poprzednich ćwiczeń, kiedy traktowaliśmy R jako kalkulator, gdy definiowaliśmy nowe obiekty lub generowaliśmy ciągi liczb. Nawet pojedyncza wartość w R jest w rzeczywistości wektorem (1-elementowym), natomiast jeśli chcemy dowolne operacje wykonywać na większej liczbie elementów wówczas musimy te obiekty złączyć za pomocą funkcji c().

Warto zaznajomić się z podstawowym cechami pracy na wektorach w celu uniknięcia późniejszych błędów.

Zadanie

  1. Stwórz wektor x o wartościach 0, 3, 2, 10, 5 oraz wektor y o wartościach 3, 4, 5. Wykonując operację dodawania, mnożenia i potęgowania na tych dwóch obiektach sprawdź jak działa autoreplikacja w R.
  2. Zmodyfikuj obiekt y tak aby zawierał tyle elementów co zmienna x, ale jako 4-ty i 5-ty element wprowadź wartości NA oznaczające brak danych. Ponownie przetestuj mnożenie na tych dwóch obiektach i sprawdź działanie autoreplikacji.
  3. Przetestuj działanie funkcji mean() oraz sum() i cumsum() na obiekcie y. Korzystając z pomocy systemowej sprawdź jak “naprawić” wynik, tak aby uwzględniał on przy obliczaniu tylko wartości liczbowe.
  4. Sprawdź działanie funkcji sort() na zmiennej x.
  5. Sprawdź działanie funkcji rev() na zmiennej y.

Staraj się przyswoić możliwie wiele funkcji omówionych do tej pory. W praktyce najczęściej stosuje się kilkadziesiąt słów kluczowych, które pozwalają na rozwiązanie większości spotykanych problemów obliczeniowych.

3.3.1 Typy danych wektorowych

W R wektory mogą przechowywać nie tylko liczby, ale także typy danych czynnikowych, datę, czas oraz ciągi tekstowe i logiczne. Póki co omówimy w dużym skrócie te 2 ostatnie, które przydadzą się w kolejnym podpunkcie.

3.3.1.1 Typ tekstowy

Deklaracja typu tekstowego odbywa się poprzez wpisanie dowolnego wyrażenia między znaki cudzysłowia " " lub w ciapkach ' '. Jeśli chcemy stworzyć obiekt przechowujący pierwsze litery alfabetu możemy go zdefiniować w następujący sposób:

c("a","b","c")
## [1] "a" "b" "c"

Warto zwrócić uwagę, że jeśli będziemy próbowali złączyć obiekty o różnych typach R domyślnie postara się je “sprowadzić” do postaci najbardziej ogólnej, co często wymusza przekonwertowanie jednego typu danych w inny:

c(1:5, "0", "5")
## [1] "1" "2" "3" "4" "5" "0" "5"

W powyższym przykładzie można rozpoznać konwersję liczb do typu tekstowego ponieważ wszystkie elementy R wydrukował w cudzysłowiach.

Wniosek: w wektorze możemy przechowywać TYLKO jeden typ danych!

3.3.1.2 Typ logiczny

Wiele procedur przetwarzania danych wymaga sprawdzania warunków logicznych, które mogą przyjmować wartości PRAWDA lub FAŁSZ. W środowisku R te wartości są deklarowane za pomocą słów TRUE lub FALSE, które można sprowadzić do skróconego zapisu dużymi literami T i F.

c(TRUE, FALSE, TRUE, FALSE) # pelne slowa
## [1]  TRUE FALSE  TRUE FALSE
c(T, F, T, F) # to samo, ale w skroconym zapisie
## [1]  TRUE FALSE  TRUE FALSE

Ciekawą własnością typu logicznego jest to, że po sprowadzeniu do wartości numerycznej (np. funkcją as.numeric()) przyjmuje ona wartości 1 (prawda) lub 0 (fałsz):

logiczny <- c(TRUE, FALSE) 
as.numeric(logiczny)
## [1] 1 0

3.3.2 Indeksowanie wektorów

Indeksowanie wektorów polega na wyborze określonych elementów obiektu poprzez wskazanie ich pozycji. Indeksy wektora w R numerowane są od 1 do n, gdzie n to długość (liczba elementów) wektora. Jeśli nie znasz długości wektora zawsze możesz ją sprawdzić za pomocą funkcji length().

Wybór dowolnych elementów wektora jest możliwy przez zastosowanie operatora [] wpisując jako argument pozycję, którą chcemy pobrać. Na początek stwórzmy wektor zawierający 20 losowych liczb z przedziału od 0 do 1. Nazwijmy ten obiekt dane i wyświetlmy jego zawartość:

dane <- runif(20)
dane
##  [1] 0.49374176 0.87379972 0.78688825 0.50432880 0.82563752 0.55914033
##  [7] 0.66054518 0.09436278 0.33954922 0.90819066 0.93333426 0.74783386
## [13] 0.19406626 0.86883230 0.11125160 0.26684243 0.07404145 0.94344484
## [19] 0.09885549 0.20364520

Komenda pozwalająca na pobranie np. tylko piątego elementu:

dane[5]
## [1] 0.8256375

Do wyświetlenia np. tylko pierwszych 10-ciu elementów musimy w nawiasie kwadratowym wprowadzić numery indeksów od 1 do 10. Wymaga to wygenerowania ciągu liczb, który będzie traktowany przez R jako ciąg liczb 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Można ten efekt osiągnąć przynajmnie na 2 sposoby.

  1. Poprzez konkatenację c():
dane[ c(1,2,3,4,5,6,7,8,9,10) ]
##  [1] 0.49374176 0.87379972 0.78688825 0.50432880 0.82563752 0.55914033
##  [7] 0.66054518 0.09436278 0.33954922 0.90819066
  1. Poprzez stworzenie ciągu liczb za pomocą operatora :
dane[ 1:10 ]
##  [1] 0.49374176 0.87379972 0.78688825 0.50432880 0.82563752 0.55914033
##  [7] 0.66054518 0.09436278 0.33954922 0.90819066

W analogiczny sposób możemy także odwrócić kolejność elementów obiektu dane wyświetlając zbiór wartości malejących od 20 do 1 z interwałem co 1:

dane[20:1]
##  [1] 0.20364520 0.09885549 0.94344484 0.07404145 0.26684243 0.11125160
##  [7] 0.86883230 0.19406626 0.74783386 0.93333426 0.90819066 0.33954922
## [13] 0.09436278 0.66054518 0.55914033 0.82563752 0.50432880 0.78688825
## [19] 0.87379972 0.49374176

Możemy także spróbować wyświetlić tylko wskazane przez nas indeksy. Jeśli chcemy wyświetlić 2 razy 10-ty element, następnie 2-gi, a potem 19-ty to możemy ponownie wykorzystać funkcję c(), która pozwala na stworzenie wektora składającego się z dowolnej konfiguracji indeksów.

dane[ c(10,10,2,19) ]
## [1] 0.90819066 0.90819066 0.87379972 0.09885549

W indeksowaniu ważne jest aby wyrażenie znajdujące się w [] było wektorem! Jeśli nie nabrałeś jeszcze wprawy w tworzeniu wektorów za pomocą c() oraz : zawsze możesz przetestować roboczo działanie wprowadzanego wyrażenia indeksującego w konsoli

W praktyce często do indeksowania wykorzystuje się inne obiekty (wektory), które zawierają numery pozycji do pobrania. Sprawdźmy to na przykładzie:

indeks <- c(1,5,10) # tworzymy wektor wartości 1, 5, 10
dane[indeks] # wyswietlamy wskazane numery, ktore sa przechowywane w obiekcie `indeks`
## [1] 0.4937418 0.8256375 0.9081907

3.3.2.1 Indeksowanie przez “negację”

Ciekawym rozwiązaniem pozwalającym w wielu przypadkach na pozbycie się niechcianych elementów jest zastosowanie jako indeksu liczb ujemnych. Jeśli chcemy pozbyć się tylko np. pierwszego elementu z naszego obiektu (np. zawiera błąd), wówczas zamiast wpisywać komendę dane[2:19] możemy ten sam efekt osiągnąć stosując poniższy zapis:

dane[-1]
##  [1] 0.87379972 0.78688825 0.50432880 0.82563752 0.55914033 0.66054518
##  [7] 0.09436278 0.33954922 0.90819066 0.93333426 0.74783386 0.19406626
## [13] 0.86883230 0.11125160 0.26684243 0.07404145 0.94344484 0.09885549
## [19] 0.20364520

Wybór poprzez eliminację nie musi się ograniczać do pojedynczego indeksu. Możliwe jest także stworzenie wektora dowolnych liczb ujemnych:

dane[c(-1,-20)] # pozbywamy sie pierwszego i ostatniego elementu
##  [1] 0.87379972 0.78688825 0.50432880 0.82563752 0.55914033 0.66054518
##  [7] 0.09436278 0.33954922 0.90819066 0.93333426 0.74783386 0.19406626
## [13] 0.86883230 0.11125160 0.26684243 0.07404145 0.94344484 0.09885549
dane[c(-5:-10, -15:-20) ] # pozbywamy sie elementow od 5. do 10. oraz od 15. do 20.
## [1] 0.4937418 0.8737997 0.7868883 0.5043288 0.9333343 0.7478339 0.1940663
## [8] 0.8688323

3.3.2.2 Indeksowanie za pomocą wyrażeń logicznych

Ciekawym rozwiązaniem przy indeksowaniu może być zastosowanie wartości logicznych TRUE lub FALSE. Na początek stwórzmy nowy wektor zawierający nazwy 4-ech losowych miast i nazwijmy go miasta.

miasta <- c("Poznań", "Wrocław", "Warszawa", "Kraków")

Stosując wektor logiczny o wartościach TRUE lub FALSE możemy indeksować, które elementy mają zostać pobrane:

miasta[c(TRUE, TRUE, FALSE, TRUE)]
## [1] "Poznań"  "Wrocław" "Kraków"

3.4 Indeksowanie z użyciem warunków logicznych

Indeksowanie jest niezmiernie ważnym elementem pracy z danymi w R. Szybkie i efektywne przetwarzenie danych wymaga testowania warunków logicznych (o tym szerzej w kolejnych częściach kursu), które pozwalają na odfiltrowanie zbiorów danych na których chcemy wykonać naszą analizę. Najczęściej sprowadza się to do stworzenia nowych obiektów (wektorów) przechowujących numery pozycji lub wartości logiczne spełniające dany test. Poniżej zamieszczono tabelę z podstawowymi operacjami logicznymi w R:

Podstawowe operatory logiczne w R
Operator Działanie operatora
< mniejsze od
<= mniejsze bądź równe
> większe od
>= większe bądź równe
== równe
!= różne od
!x negacja
x | y suma logiczna zbiorów
x & y iloczyn logiczny zbiorów

3.4.1 Testowanie warunków logicznych

Działanie operatorów logicznych najlepiej sprawdzić w praktyce. Na początek stwórzmy obiekt dane2, w którym będziemy przechowywać 30 losowych wartości od -1 do +1 i wyświetlmy jego zawartość

dane2 <- runif(n = 30, min = -1, max = 1)
dane2
##  [1] -0.59560858 -0.25663961 -0.68450414 -0.95169447 -0.47746910
##  [6]  0.20173057 -0.80483792  0.18520535  0.30800409 -0.32567132
## [11] -0.85185257  0.40434589 -0.42623454 -0.93771629  0.29577374
## [16] -0.14254649 -0.59012426  0.16720433  0.46219250  0.43996621
## [21]  0.91914229  0.08958197  0.07898348  0.87232260  0.29511599
## [26]  0.83302244 -0.65629381  0.05567291 -0.56115267 -0.66073267

Sprawdzenie, które liczby są większe bądź równe 0 jest możliwe poprzez zastosowanie komendy:

dane2 >= 0
##  [1] FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE  TRUE FALSE FALSE
## [12]  TRUE FALSE FALSE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE
## [23]  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE FALSE

Otrzymany wynik 30-tu wartości (TRUE/FALSE) wskazuje czy w danym indeksie wartość spełnia dany warunek logiczny. Jeśli chcemy się pozbyć wartości ujemnych możemy np. stworzyć wektor wartości logicznych, zapisać go jako nowy obiekt i podstawić jako indeks:

indeks <-  dane2 >= 0        #   tworzymy wektor indeksujacy
dane2 [ indeks ]
##  [1] 0.20173057 0.18520535 0.30800409 0.40434589 0.29577374 0.16720433
##  [7] 0.46219250 0.43996621 0.91914229 0.08958197 0.07898348 0.87232260
## [13] 0.29511599 0.83302244 0.05567291

Lub z pominięciem etapu tworzenia tymczasowego obiektu indeksującego:

dane2 [ dane2 >= 0 ]
##  [1] 0.20173057 0.18520535 0.30800409 0.40434589 0.29577374 0.16720433
##  [7] 0.46219250 0.43996621 0.91914229 0.08958197 0.07898348 0.87232260
## [13] 0.29511599 0.83302244 0.05567291

3.4.2 Funkcja which

W wielu przypadkach bardziej wygodna w użyciu będzie funkcja which() (ang. “który”) zwracająca numery pozycji spełniających dany warunek logiczny.

which() (ang. “który/które”) - czyli które elementy spełniają dany warunek logiczny.

Poniższa komenda wskazuje indeksy wektora dane2 większe od 0

which(dane2>0)
##  [1]  6  8  9 12 15 18 19 20 21 22 23 24 25 26 28

Możemy także jednorazowo wykonać 2 testy logiczne, takby aby wybrać np. liczby które są jednocześnie większe bądź równe -0.5 i mniejsze bądź równe -0.1. Graficznie taką zależność możemy wyobrazić sobie jako znalezienie elementów, które zawierają się w niebieskim prostokącie.

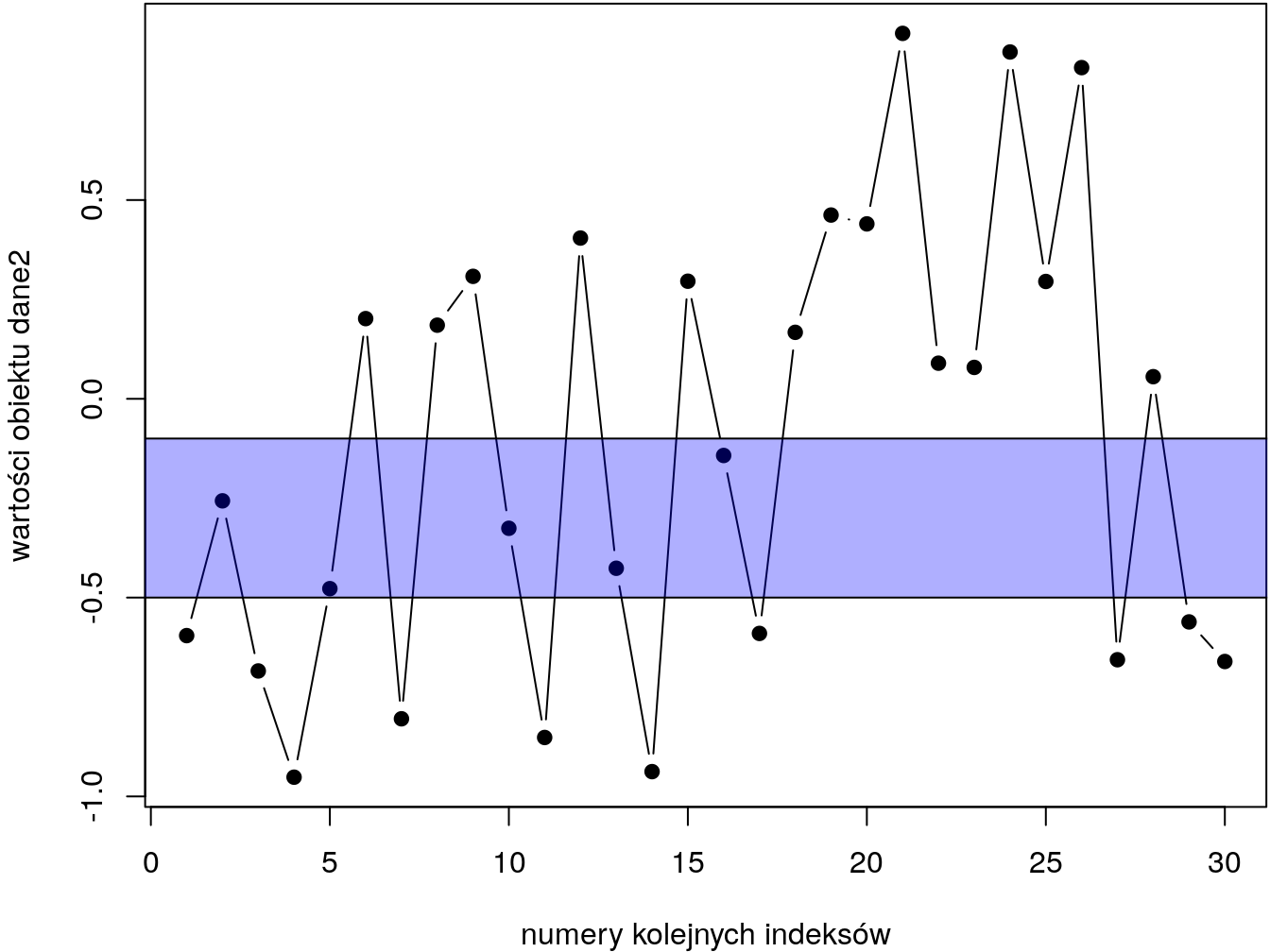
Znajdowanie liczb znajdujących się w przedziale domkniętym od -0.5 od -0.1.

Rysunek 3.1: Znajdowanie liczb znajdujących się w przedziale domkniętym od -0.5 od -0.1.

Odszukanie indeksów tych elementów w składni R jest możliwe z wykorzystaniem wyrażeń logicznych i funkcji which()

which(dane2 >= -0.5 & dane2 <= -0.1 )
## [1]  2  5 10 13 16

Operator & oznacza iloczyn logiczny zbioru. Jeśli interesowałyby nas wartości, które są jednocześnie mniejsze od -0.5 LUBsą większe od 0.5 (jak na rys. 3.2 ), wówczas zamiast iloczynu logicznego powinniśmy użyć sumy logicznej zbioru (czyli operatora |).

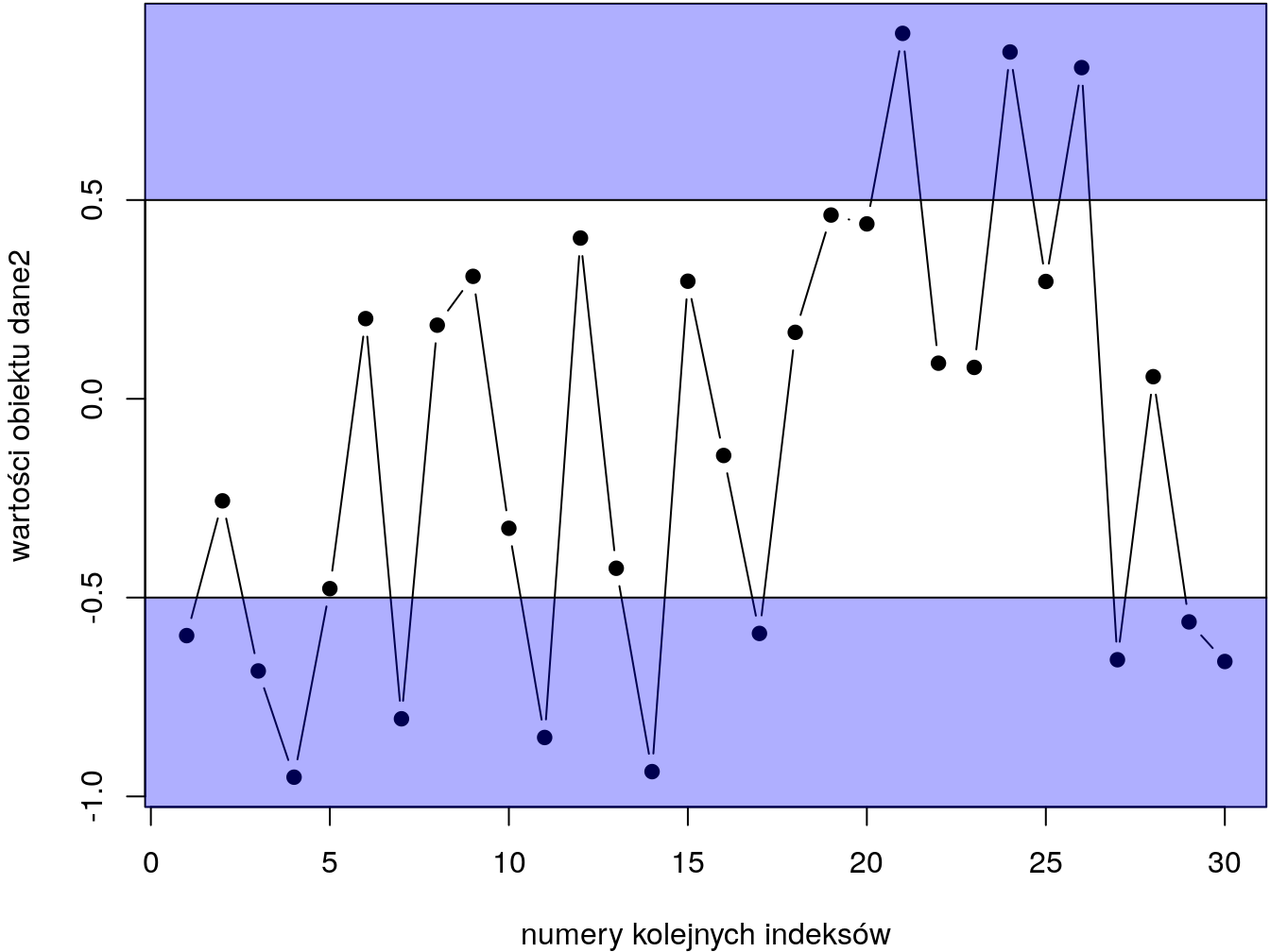
Znajdowanie wartości mniejszych od -0.5 i większych od 0.5

Rysunek 3.2: Znajdowanie wartości mniejszych od -0.5 i większych od 0.5 

which(dane2< -0.5 | dane2> 0.5)
##  [1]  1  3  4  7 11 14 17 21 24 26 27 29 30

Jeśli interesują nas same wartości spełniające dany warunek logiczny (a nie indeksy) możemy zapisać wynik powyższego działania do nowego obiektu i wykorzystać go jako wektor indeksujący

indeks <- which(dane2< -0.5 | dane2> 0.5)
dane2[indeks]
##  [1] -0.5956086 -0.6845041 -0.9516945 -0.8048379 -0.8518526 -0.9377163
##  [7] -0.5901243  0.9191423  0.8723226  0.8330224 -0.6562938 -0.5611527
## [13] -0.6607327

Jeśli chcemy wyświetlić wszystkie pozostałe wartości możemy postawić znak minus w [] , co da nam wartości indeksu pomnożone razy -1

dane2[-indeks] # lub to samo zapisane jako: dane2[indeks * -1]
##  [1] -0.25663961 -0.47746910  0.20173057  0.18520535  0.30800409
##  [6] -0.32567132  0.40434589 -0.42623454  0.29577374 -0.14254649
## [11]  0.16720433  0.46219250  0.43996621  0.08958197  0.07898348
## [16]  0.29511599  0.05567291

3.5 Zadania podsumowujące

3.5.1 Skrypt

  1. Utwórz nowy skrypt i skopiuj do niego zawartość kodu ze strony: [http://enwo.pl/przetwarzanie/lorenz.r] (http://enwo.pl/przetwarzanie/lorenz.r)

  2. Uruchom skrypt

3.5.2 Tworzenie wektorów

  1. Stwórz wektor miasta składający z 3-ech losowych nazw miejscowości.

  2. Dołącz do obiektu miasta kolejne o nazwie Wzdół Rządowy [1], [2 ].

  3. Nadpisz zawartość wektora miasta usuwając ostatnią nazwę, gdyż Wzdół Rządowy jest wsią a nie miastem.

3.5.3 Indeksowanie

  1. Wyświetl zawartość wbudowanej zmiennej letters

  2. Jaka jest 24-ta litera alfabetu zapisanego w obiekcie letters?

  3. Ile liter jest dalej w alfabecie niż litera s ? Wykorzystaj zapytanie logiczne >

Przydatna może być także wiedza o wartościach numerycznych dla TRUE/FALSE oraz funkcji sum().

  1. Korzystając z operatora [] wyświetl:
  1. parzyste litery alfabetu (2,4,6 …)
  2. nieparzyste litery alfabetu (1,3,5 …)

5.1. Stwórz obiekty lon i lat zawierające wartości południków (lon) i równoleżników (lat) dla obszaru Europy odpowiadającej siatce modelu GFS. Model GFS ma rozdzielczość przestrzenną 0.25 x 0.25 stopnia. Przyjmij roboczo, że obszar Europy zawiera się w od 25W do 40E oraz od 30N do 75N (rys. 3.3 ). Dla oznaczenia długości geograficznej przyjmij wartości ujemne dla długości geograficznej zachodniej (tj. 25W = -25) i dodatnie dla długości geograficznej wschodniej (tj. 40E = 40). Kontrolnie możesz sprawdzić długość powstałych obiektów (funkcją length()). Sprawdź czy stworzono 261 południków i 181 równoleżników.

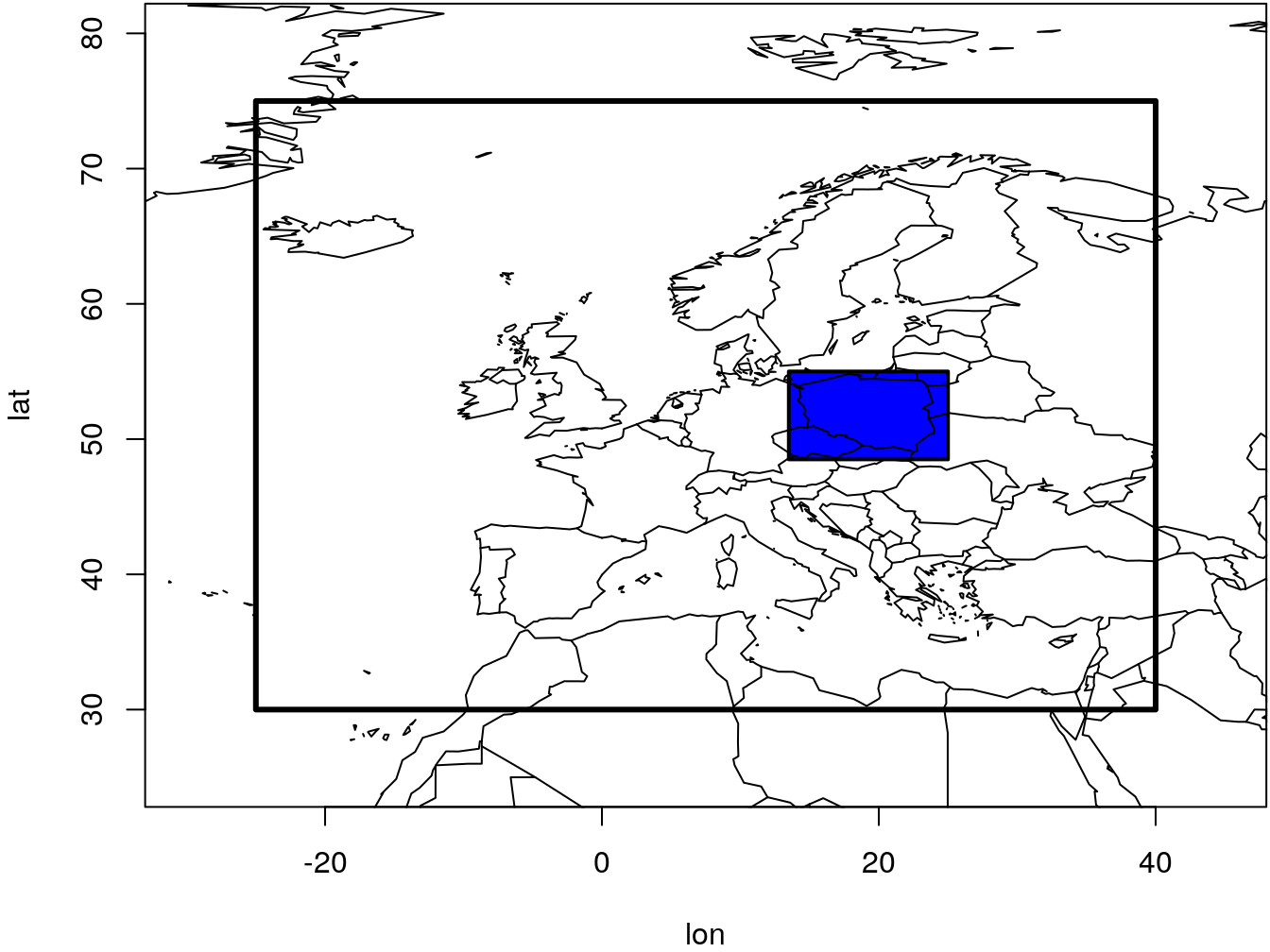
Schemat domeny obliczeniowej modelu GFS dla Europy

Rysunek 3.3: Schemat domeny obliczeniowej modelu GFS dla Europy

5.2. Za pomocą funkcji which() wskaż numery indeksów lon i lat, które zawierają obszar Polski (3.3 ). Przyjmij roboczo, że długości geograficzne powinny zawierać się w przedziale od 13.5 do 25, a szerokości od 48.5 do 55.

5.3. Z obiektów lon i lat wydobądź poprzez operator [ ] wartości południków i równoleżników w podanym powyżej zakresie (13.5E-25.0E, 48.5N-55.0N). Wartości zapisz do nowych obiektów lon2 i lat2.

5.4. Ile elementów zawierają nowe obiekty lon2 i lat2 ?

Zadanie domowe

  1. Korzystając z wbudowanego systemu pomocy puść “totolotka” za pomocą funkcji sample() generując zestaw liczb od 1 do 49, a następnie wywołując parametr size= dla sześciu liczb.
  2. Wygeneruj i zapisz w postaci wektora dowolny ciąg liczbowy składający się z 20-50 liczb. Następnie korzystając z wygenerowanych liczb i wbudowanego systemu pomocy przetestuj działanie poniższych funkcji:
Wybrane funkcje uzupełniające niezbędną wiedzę do pracy na wektorach w R
Nazwa funkcji Działanie
summary() statystyki podsumowujące
range() zwraca jednocześnie minimalną i maksymalną wartość
rev() odwraca kolejność elementów
rep() replikacja / powtarzanie / zwielokrotnienie
sort() sortowanie
length() długość obiektu

Zadania sprawdzające